Mutlak Değer konusu hem kısa hemde anlaşılması kolay konulardandır. Yapmanız gereken tek şey Mutlak Değer konusuna çalıştıktan hemen sonra pekiştirme amaçlı soru çözümü yapmaktır. Yeterli sayıda soru çözdükten sonra artık Mutlak Değer konusuyla ilgili herhangi bir zorluk yaşayacağınızı düşünmüyoruz.
Mutlak Değer konusu ile ilgili ders notları ve konu anlatımını sizler için aşağıda derledik.
MUTLAK DEĞER :
Bir reel sayının, sayı doğrusu üzerinde eşlendiği noktanın başlangıç noktasına olan uzaklığına sayının mutlak değeri denir.
Bir x reel sayısının mutlak değeri |x| biçiminde gösterilir.
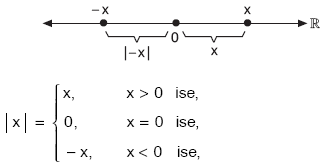
NOT: Bütün x gerçel (reel) sayıları için, |x| ³ 0 dır.
B. MUTLAK DEĞERİN ÖZELİKLERİ
|x| = |–x| ve |a – b| = |b – a| dır.
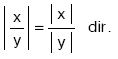
|x| = a ise, x = a veya x = –a dır.
|x – a| + |x – b|
ifadesinin en küçük değeri a £ x £ b koşuluna uygun bir x değeri için bulunan sonuçtur.
K = |x – a| – |x – b|
olmak üzere,
x = a için K nin en küçük değeri, x = b için K nin en büyük değeri bulunur.
a) |x| < a ise, –a < x < a dır.
b) |x| £ a ise, –a £ x £ a dır.
a) |x| > a ise, x < –a veya x > a dır.
b) |x| ³ a ise, x £ –a veya x ³ a dır.
|x + a| + |x + b| = c
eşitliğinin çözüm kümesini bulmak için 2 yöntem vardır.
1. Yöntem
Mutlak değerlerin içlerinin kökleri bulunur.
x + a = 0 ise, x = –a dır.
x + b = 0 ise, x = –b dir.
Buna göre, üç durum vardır. (–b < –a olsun.)
–b £ x, –b < x £ –a ve x > –a dır. Bu üç durumda inceleme yapılır.
1. Durum –b £ x ise, –x – a – x – b = c olur. Bu denklemin kökü –b £ x koşulunu sağlıyorsa, verilen denklemin de köküdür.
2. Durum –b < x £ –a ise, –x – a + x + b = c olur.
Bu denklemin kökü –b < x £ –a koşulunu sağlıyorsa, verilen denklemin de köküdür.
3. Durum x > –a ise, x + a + x + b = c olur. Bu denkleminin kökü x > –a koşulunu sağlıyorsa, verilen denklemin de köküdür.
3 durumdan elde edilen köklerin oluşturacağı küme, verilen denklemin çözüm kümesidir.
2. Yöntem
a < b ve c Î R olmak üzere,
|x + a| + |x + b| = c … (¶)
eşitliğinin çözüm kümesinde aşağıdaki üç durum geçerlidir.
(x + a = 0 ise, x = –a) ve (x + b = 0 ise, x = –b)
(¶) daki denklemin çözüm kümesi,
Ç = [–b, –a] dır.
(¶) daki denklemin çözüm kümesi,
Ç = Æ dir.
(¶) daki denklemi sağlayan iki sayı vardır. Bu sayıları bulmak için, c den, sayı doğrusunda –b ile –a arasındaki uzaklık çıkarılır, farkın yarısı bulunur. Son bulunan değer D olsun. Buna göre, (¶) daki denklemi sağlayan sayılardan biri –b – D diğeri –a + D dir. Bu durumda (¶) daki denklemin çözüm kümesi,
Ç {–b – D, –a + D} olur.
Mutlak Değer konusu ile ilgili ders notları ve konu anlatımını sizler için aşağıda derledik.
MUTLAK DEĞER :
Bir reel sayının, sayı doğrusu üzerinde eşlendiği noktanın başlangıç noktasına olan uzaklığına sayının mutlak değeri denir.
Bir x reel sayısının mutlak değeri |x| biçiminde gösterilir.

NOT: Bütün x gerçel (reel) sayıları için, |x| ³ 0 dır.
B. MUTLAK DEĞERİN ÖZELİKLERİ
|x| = |–x| ve |a – b| = |b – a| dır.
- |x × y| = |x| × |y|
- |xn| = |x|n
- y ¹ 0 olmak üzere,
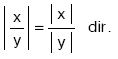
- |x| – |y| £ |x + y| £ |x| + |y|
- a ³ 0 ve x Î R olmak üzere,
|x| = a ise, x = a veya x = –a dır.
- |x| = |y| ise, x = y veya x = –y dir.
- x değişken a ve b sabit birer reel (gerçel) sayı olmak üzere,
|x – a| + |x – b|
ifadesinin en küçük değeri a £ x £ b koşuluna uygun bir x değeri için bulunan sonuçtur.
- x değişken a ve b sabit birer reel (gerçel) sayı ve
K = |x – a| – |x – b|
olmak üzere,
x = a için K nin en küçük değeri, x = b için K nin en büyük değeri bulunur.
- a, pozitif sabit bir reel sayı olmak üzere,
a) |x| < a ise, –a < x < a dır.
b) |x| £ a ise, –a £ x £ a dır.
- a, pozitif sabit bir reel sayı olmak üzere,
a) |x| > a ise, x < –a veya x > a dır.
b) |x| ³ a ise, x £ –a veya x ³ a dır.
- a < b ve c Î R olmak üzere,
|x + a| + |x + b| = c
eşitliğinin çözüm kümesini bulmak için 2 yöntem vardır.
1. Yöntem
Mutlak değerlerin içlerinin kökleri bulunur.
x + a = 0 ise, x = –a dır.
x + b = 0 ise, x = –b dir.
Buna göre, üç durum vardır. (–b < –a olsun.)
–b £ x, –b < x £ –a ve x > –a dır. Bu üç durumda inceleme yapılır.
1. Durum –b £ x ise, –x – a – x – b = c olur. Bu denklemin kökü –b £ x koşulunu sağlıyorsa, verilen denklemin de köküdür.
2. Durum –b < x £ –a ise, –x – a + x + b = c olur.
Bu denklemin kökü –b < x £ –a koşulunu sağlıyorsa, verilen denklemin de köküdür.
3. Durum x > –a ise, x + a + x + b = c olur. Bu denkleminin kökü x > –a koşulunu sağlıyorsa, verilen denklemin de köküdür.
3 durumdan elde edilen köklerin oluşturacağı küme, verilen denklemin çözüm kümesidir.
2. Yöntem
a < b ve c Î R olmak üzere,
|x + a| + |x + b| = c … (¶)
eşitliğinin çözüm kümesinde aşağıdaki üç durum geçerlidir.
(x + a = 0 ise, x = –a) ve (x + b = 0 ise, x = –b)
- Sayı doğrusunda –b ile –a arasındaki uzaklık c ye eşit ise,
(¶) daki denklemin çözüm kümesi,
Ç = [–b, –a] dır.
- Sayı doğrusunda –b ile –a arasındaki uzaklık c den büyük ise,
(¶) daki denklemin çözüm kümesi,
Ç = Æ dir.
- Sayı doğrusunda –b ile –a arasındaki uzaklık c den küçük ise,
(¶) daki denklemi sağlayan iki sayı vardır. Bu sayıları bulmak için, c den, sayı doğrusunda –b ile –a arasındaki uzaklık çıkarılır, farkın yarısı bulunur. Son bulunan değer D olsun. Buna göre, (¶) daki denklemi sağlayan sayılardan biri –b – D diğeri –a + D dir. Bu durumda (¶) daki denklemin çözüm kümesi,
Ç {–b – D, –a + D} olur.


